Introduction

We've seen in the previous post that the noises we want have special properties. Here, we'll write a noise function that have those, called the value noise.

In this post, we'll see :

1. how to have reproducible pseudo-random generator for integers,
2. how to transform that into a smooth noise for real numbers with an interpolation,
3. hot to make a simple implementation of this value noise in Rust.

This post is considerably longer than the previous one, because I wanted to explain everything about value noise in one dimension. I think it's important, as value noise in higher dimensions and other noises work in similar ways.

There's a lot in this post and remember that it's normal to not understand everything the first time. Take your time. Read again or ask me some questions if there's something you don't understand.

Have a good reading !

1 : Reproductibility

One important property we want is reproductibility. I'll take an example in 1D and with integers numbers only. We want a function, some kind of blackbox for which, given some number \(n\), returns a value \(f(n)\). For the same \(n\), this function will always return \(f(n)\) and nothing else.

This is the opposite of a random value, you might say. Indeed, this is not random at all, but what's important is that our function gives the feeling of randomness. Let's face it, computers and algorithms cannot generate pure randomness, but we can produce something that looks like it. This is known as pseudo-randomness.

There's a lot to say about pseudo-randomness and random number generators, and it's a very complicated subject with a lot of maths. But that's not the subject of this post.

Concretely, what would make \(n \rightarrow f(n)\) a pseudo-random function ? Let's say that for us, \(n \rightarrow f(n)\) is a pseudo-random function if for all \(n\), the value of \(f(n+1)\) is not correlated, not influenced by the value of \(f(n)\). There is no patterns to see between the successive values of \(f\).

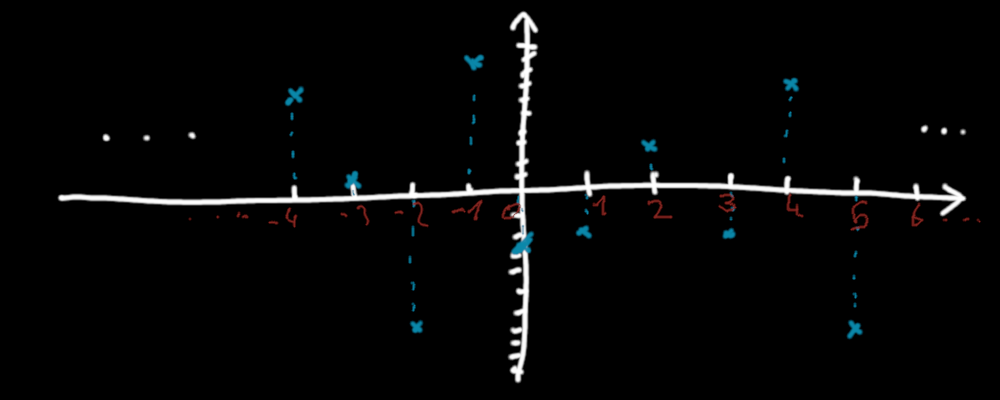
A function defined for integers that seems to be random.

Programming languages typically implement some random functions... But not the kind we want. They take no arguments, just every time you call these functions, they'll give a new random value.

• first call -> random value 1
• second call -> random value 2
• third call -> random value 3
• etc...

But this is not equivalent to :

• \(f(1)\) -> random value 1
• \(f(2)\) -> random value 2
• \(f(3)\) -> random value 3
• etc...

In particular, if I ask for the value of \(f(1)\) twice, I'll get :

• first call for \(f(1)\) -> random value 1
• second call, but also for \(f(1)\) -> random value 2

The value of \(f(1)\) has changed ! So, we have to find our own ways of producing pseudo-random values.

1.1 : Integer noise function

There exists functions that seems to give pseudo-random numbers, always the same if we give the same input. The result will also always be between -1 and 1. They are almost noise functions, except that they are defined on the integers instead of the real numbers.

An example is given by libnoise, here in C:

double IntegerNoise (int n)
{
  n = (n >> 13) ^ n;
  int nn = (n * (n * n * 60493 + 19990303) + 1376312589) & 0x7fffffff;
  return 1.0 - ((double)nn / 1073741824.0);
}

That looks like magic, and in a way, it is. Don't worry if you don't understand it, it's really not important.

A little help if you still want to understand : all the integers numbers above are prime. They ensure that there will be no discernible patterns in the return of the function. nn will be a huge number wrapped around the maximum value of a 32-bit integer and masked to be positive. Finally, the value is divided by the maximum of a 32-bit integer, divided by two ; thus the result is between -1 and 1, seems random, and will always be the same with the same input n.

Here is a Rust equivalent with other prime numbers :

fn integer_noise(&n: &i32) -> f64 {
    let nn: i32 = (n << 13) ^ n;
    let nn: i32 = (nn
        .wrapping_mul(nn.wrapping_mul(nn.wrapping_mul(15731)).wrapping_add(789221))
        .wrapping_add(1376312589))
        & 0x7fffffff;
    return 1.0 - (nn as f64 / 1073741824.0);
}

It seems more complicated because in Rust the result of an operation between integers is not wrapped around the maximum value by default.

The result for the integers between -4 and 5 :

n = -4, integer noise is 0.5935161774978042
n = -3, integer noise is 0.12301606219261885
n = -2, integer noise is -0.703192631714046
n = -1, integer noise is 0.9001262886449695
n = 0, integer noise is -0.2817909838631749
n = 1, integer noise is -0.2263730512931943
n = 2, integer noise is 0.29363288078457117
n = 3, integer noise is -0.2571851881220937
n = 4, integer noise is 0.585760741494596
n = 5, integer noise is -0.7129413308575749

Some values of our integer noise.

1.2 : Hash function

The previous way works great, but it's a little bit too complex. There's a simpler way, called hash functions, to have random values over the integers, with some trade-offs.

The trade-offs are :

• the hash function is periodic : there exists a number \(N\) for which \(f(N+i) = f(i), \forall i \in \mathbb{N}\) (the function repeats itself every \(N\) steps). This could be a problem, but in practice for a large, known \(N\), this is not a real (visible) problem.
• the hash function gives regularly spaced values : \(\forall i \in \mathbb{N}, f(i) = 1 - 2 \frac{k}{N-1}\), for some \(k \in [0;N-1]\). Again, this could be a problem, but in practice for a large, known \(N\), this is not a real (visible) problem.

In the next picture, we do see the trade-offs because the periodicity \(N=9\) is small. We feel that each value is placed "on a grid" and we see the pattern repeating itself quickly.

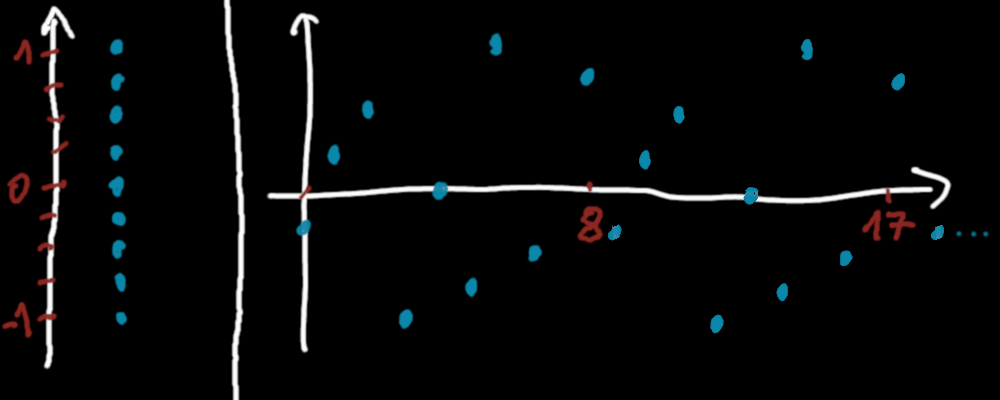
Left : the only possible values for a specific hash function. Right : it's periodicity is 9.

But if we restrict ourselves on the interval \([0;N-1]\), the feeling of random is correct. One might even say that it's a little bit too perfect because each possible value is obtained exactly once on this interval. That's also another property of the hash function.

Permutation tables

One way to obtain a hash function is to use a permutation table. The concept is very simple. In an array, take all the number between \(0\) and \(N-1\).

For example with \(N = 9\) :

perm = [0, 1, 2, 3, 4, 5, 6, 7, 8]

Now, shuffle randomly this array :

perm = [5, 3, 2, 8, 4, 7, 0, 6, 1]

We define the hash function \(f\) of periodicity \(N=9\) defined on \(\mathbb{Z}\) by : \[f(i) = 1 - 2 \frac{perm[i\mod9]}{8}\]

which gives the following function between \(0\) and \(N-1\):

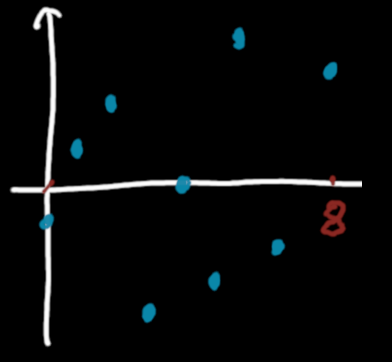
Our hash function between 0 and N-1.

Once again, here we do see the trade-offs, but they are not visible with a large value for \(N\).

The hash function is entirely determined by the shuffled array. If we shuffled it differently, the hash function would be different. If we want to have reproducible values between each execution of our code, we must make sure that the array is always shuffled the same way.

• either we write directly the shuffled array into the code,
• either we use a random shuffle algorithm, but we make sure to fix the seed of the random number generator before that. The seed will "reset" the random values given by the random number generator used to shuffle. See this wikipedia article if you want to know more about seeds.

For example, in Rust with a periodicity of 256, using the random_chacha crate :

// trait for shuffling
use rand::seq::SliceRandom;
// trait to construct a pseudo random number generator with a fixed seed.
use rand::SeedableRng;

let seed = 12; // fix a seed somewhere

// our *seeded* random number generator
let mut rng = rand_chacha::ChaCha20Rng::seed_from_u64(seed);

let mut p = [0; 256];
for i in 0..256 {
    p[i] = i as usize;
}
p.shuffle(&mut rng);
for i in 0..256 {
    print!("{}, ", p[i]);
}

[145, 27, 50, 39, 74, 41, 239, 12, 227, 186, 47, 215, 18, 80, 159, 172, 17, 117, 212, 101, 249, 65, 193, 198, 166, 2, 137, 38, 233, 190, 135, 86, 205, 56, 121, 21, 223, 242, 149, 143, 173, 52, 91, 54, 170, 107, 157, 66, 154, 64, 192, 72, 202, 196, 106, 49, 127, 194, 124, 26, 105, 218, 78, 222, 123, 131, 61, 221, 119, 199, 251, 136, 245, 200, 171, 10, 24, 113, 5, 208, 0, 197, 165, 133, 150, 23, 57, 128, 180, 32, 236, 69, 178, 109, 232, 11, 195, 201, 46, 234, 71, 14, 103, 55, 230, 182, 77, 206, 81, 126, 243, 160, 85, 40, 9, 92, 84, 37, 153, 89, 141, 15, 93, 114, 102, 34, 161, 73, 229, 111, 235, 163, 108, 53, 76, 226, 189, 164, 25, 183, 140, 7, 177, 19, 209, 151, 116, 96, 130, 162, 98, 167, 247, 6, 138, 36, 68, 59, 228, 83, 48, 3, 238, 188, 94, 207, 181, 244, 240, 120, 125, 185, 99, 87, 179, 43, 104, 112, 142, 254, 35, 97, 139, 241, 255, 31, 67, 250, 44, 156, 213, 176, 217, 8, 214, 184, 115, 16, 110, 216, 45, 203, 158, 100, 155, 51, 175, 252, 174, 79, 231, 211, 219, 246, 75, 187, 132, 147, 30, 204, 62, 168, 225, 4, 1, 210, 13, 134, 70, 152, 122, 148, 82, 29, 58, 42, 191, 169, 33, 248, 95, 88, 22, 224, 118, 220, 144, 146, 28, 253, 237, 20, 90, 60, 129, 63]

2 : Getting real with interpolation

Now that we have a way to produce pseudo-random numbers between -1 and 1 on all the integers, we'll extend that on the real numbers. Here is the idea of the Value Noise in 1D :

• each real number is between two integers,
• at each integers, we can assign a random value between -1 and 1 thanks to our hash function,
• the value we'll assign to any real number is the interpolation (understand "a mix of") between the values of the hash function for the integer before and after the real number.

There's several ways to mix two values. We'll see first the simplest : the linear interpolation.

2.1 : Linear interpolation

Consider the following situation :

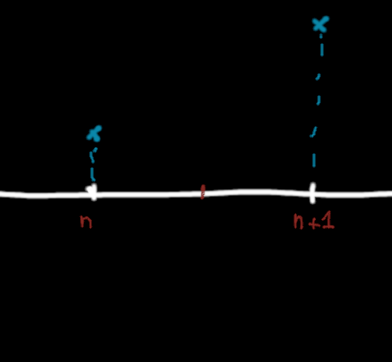
How to construct the linear interpolation between two points ?

What would be the simplest way to "guess" the value of a point in the middle of the two given points ? More generally, what the function passing through these two points could look like ? The simplest answer is to draw a straight line between these two known points.

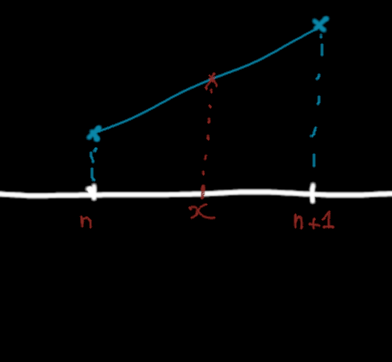
A linear interpolation between two points.

Now, if you want to know the value of your function in between, you just have to look where the point in between lies on the straight line.

Mathematically, we want to construct, parts by parts, a continuous function \(f\). A part here is an interval between two integers, say \(n\) and \(n+1\). We know the values of \(f(n)\) and \(f(n+1)\) and we want to linearly interpolate the value of the function \(f\) at some point \(z \in ]n;n+1[\).

For simplicity, we'll ask the value of \(f(n+x), x \in ]0;1[\), which is equivalent.

• if \(x = 0\), we know the value of \(f\) : it's \(f(n)\).
• if \(x = 1\), we know the value of \(f\) : it's \(f(n+1)\).
• if \(x\) is in between, we have to follow the slope of the straight line through \(f(n)\) and \(f(n+1)\).
• the slope of the straight line through \(f(n)\) and \(f(n+1)\) is \(\frac{\Delta y}{\Delta x} = \frac{f(n+1) - f(n)}{(n+1)-n} = f(n+1)-f(n)\)
• \(f(n+x) = f(n) + x(f(n+1)-f(n)) = xf(n+1) + (1-x)f(n)\)

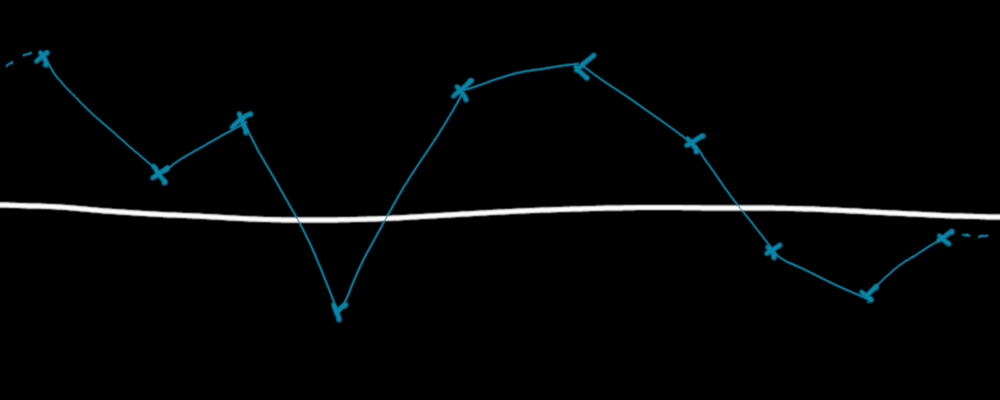
A linearly interpolated function between random given points. It's linear by parts and continuous.

Notice the previous picture.

• The values of the function are random at a large scale, however it's continuous so a small change in the input will only produce a small change in the output. That's a property of a coherent noise.
• By using the hash function we've seen with a fixed permutation table, we have a reproducible function, because then all the integer values are fixed, and so the interpolation between them is fixed too.
• All the values are between -1 and 1 because the fixed integer values are between -1 and 1 and the interpolation will always give values between them.

We have almost all the properties to consider this function a noise in one dimension ! It lacks only two properties :

• The function is not very smooth. At each integer value, there is an "angle".
• We still haven't talk about the fractal part... this is on purpose. This point is the least important and having a simple noise function will ensure that we can fractalize it in the future.

2.2 : Quintic Hermite Spline : a smoother interpolation

We have almost everything to make our Value Noise, which is just smoother. It just uses another type of interpolation, not with straight lines, but with smooth curves :

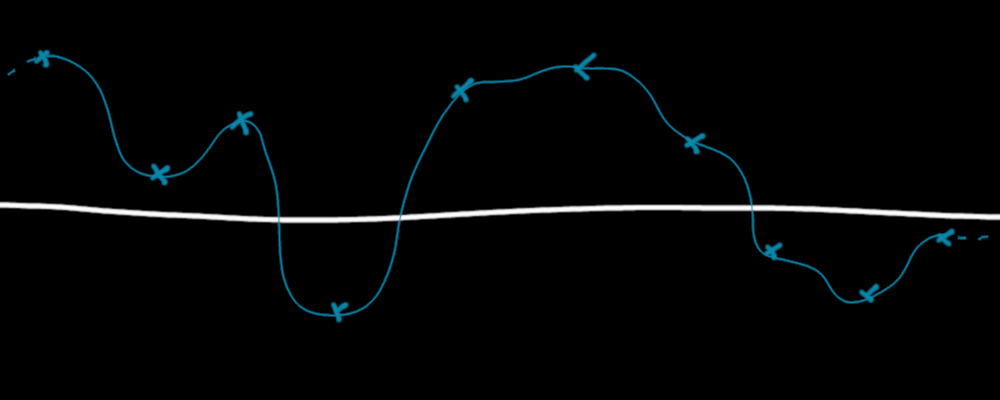
An interpolated function between random given points. It's smooth and continuous.

The idea is quite the same : we mix the value between two points, but not by drawing a straight line between them. We ensure that the derivative of the function is also continous at each point. In particular at the "control points", those where we know the value. To avoid the angles we have with linear interpolation, we want to have the same left and right derivative at those points.

As we want to use always the same interpolation between each control points, and we would like to have the guarantee that each interpolated value is in between the values at the control points, we only have one choice : we have to ensure that the value of the derivative at the control points is 0 (as the hash function at control points gives values between -1 and 1, and we want a noise between these bounds, it's important to make sure that the interpolated values are strictly within these bounds).

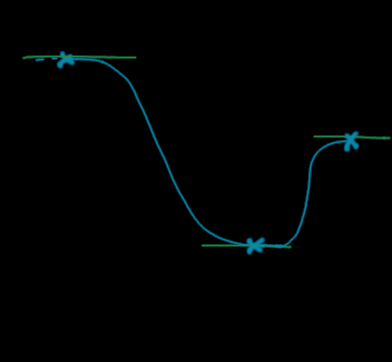
The effect of setting a zero derivative at each integer value.

Just by doing that, we have a smoother function, there will be no angles at each integer values, just a flat, smooth transition. We can do even better by setting the second derivative to zero, which might be important in some applications of the noise function. A classical solution for interpolation with null first and second derivative at control points is the quintic Hermite spline defined by \(s(t) = 6t^5 - 15t^4 + 10t^3\). It looks like this :

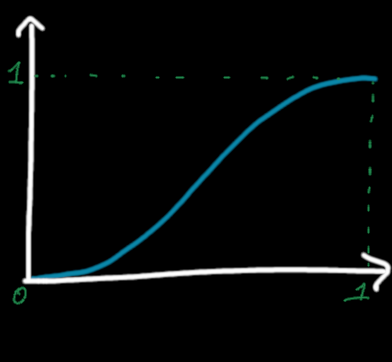
Quintic Hermite spline between 0 and 1.

Let's verify that the first and second derivatives of this function are null at \(t=0\) and \(t=1\).

First derivative : \[s'(t) = 5 \times 6t^4 - 4 \times 15t^3 + 3 \times 10t^2 = 30t^4 - 60 t^3 + 30t^2\]

\[s'(0) = 30 \times 0^4 - 60 \times 0^3 + 30 \times 0^2 = 0\]

\[s'(1) = 30 \times 1^4 - 60 \times 1^3 + 30 \times 1^2 = 30 - 60 + 30 = 0\]

Second derivative : \[s''(t) = 4 \times 30t^3 - 3 \times 60 t^2 + 2 \times 30t = 120t^3 - 180t^2 + 60t\]

\[s''(0) = 120 \times 0^3 - 180 \times 0^2 + 60 \times 0 = 0\]

\[s''(1) = 120 \times 1^3 - 180 \times 1^2 + 60 \times 1 = 120 - 180 + 60 = 0\]

Doing an interpolation with the quintic Hermite spline is not so hard. It's almost like the linear interpolation case : we just say "I want a proportion, say \(1-h(x)\) of the first point, and a proportion \(h(x)\) of the second point".

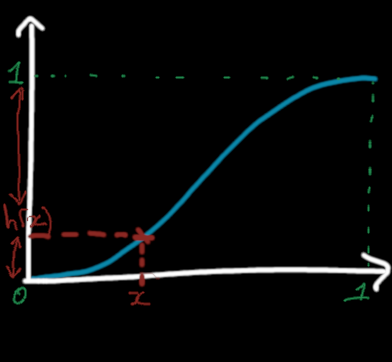
Quintic hermite spline between 0 and 1. We ask for a mix with proportion 1-h(x) and h(x).

In Rust, we could code a function to return the quintic hermite spline interpolation between two values of a function on two integers by just giving the value \(x \in [0;1]\) that determines the proportions.

fn quintic_interpolation(x: f64, f1: f64, f2: f64) -> f64 {
  // just a way to compute the quintic Hermite spline with additions and multiplications only
  let h_of_x = x * x * x * (x * (x * 6.0 - 15.0) + 10.0);
  return (1.0 - h_of_x) * f1 + h_of_x * f2;
}

Note that with both the linear and the quintic interpolation, the maximum value of the interpolated function between \(n\) and \(n+1\) is either \(f(n)\) or \(f(n+1)\).

3 : 1D Value Noise

We did a long journey to get there, but this is it. We are finally ready to implement the Value Noise ! In one dimension, it will give results that look like this :

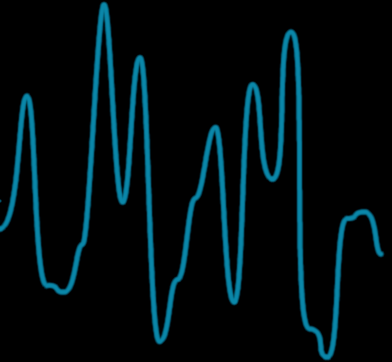
A taste of what the 1D value noise looks like.

Notice how beautiful it is ! It's random, but also coherent as in smooth and continuous, and it's always between -1 and 1 ! Furthermore, it only depends on a seed to shuffle once a permutation table. The seed fixed, the results are reproducible : asking for the noise at the point \(113.12\) will always give the same value, for example.

So how do we do it ?

1. We fix a seed.
2. We use that seed to apply a random permutation between 0 and \(N\). We'll use the classical value of \(N = 255\).
3. This permutation allows us to define a hash function that associates to each integer a pseudo-random value between -1 and 1.
4. Then, for a given real input value \(x\), we look at the nearest integers at its left and right and interpolate their values from the hash function to give the value noise at \(x\).

We'll make a simple implementation in Rust. First, we create a new Struct named "ValueNoise", with only one attribute : the permutation table.

pub struct ValueNoise {
    perm: [usize; 256]
}

When creating an object of instance ValueNoise, we'll always give a number, the seed to configure a pseudo-random number generator used to make the permutation table. The random generator comes from the rand_chacha crate.

// trait for shuffling
use rand::seq::SliceRandom;
// trait to construct a pseudo random number generator with a fixed seed.
use rand::SeedableRng;

impl ValueNoise {
    // Create and return a new value noise object
    pub fn new(seed : u64) -> Self {
        // seeding the pseudo-random number generator
        let mut rng = rand_chacha::ChaCha20Rng::seed_from_u64(seed);
        let mut perm = [0; 256];
        //perm = [0, 1, 2, ..., 254, 255]
        for i in 0..256 {
            perm[i] = i as usize;
        }
        // we shuffle the array
        perm.shuffle(&mut rng);
        // we return a new Value Noise object with a shuffled array ready to be used in the hash function
        return Self {perm: perm};
    }
}

Finally, let's write the noise function :

impl ValueNoise {
    // value noise at x
    pub fn noise1D(&self, x: f64) -> f64 {
        // left integer is intx
        let intx: f64 = x.floor();
        // Next we shift the coordinates such that x is between 0 and 1
        let x: f64 = x - intx;
        // We wrap the integer around a maximum of 255
        let intx: usize = (intx as usize) % 255;

        // What are the values of the hash function for the index intx (integer to the left of x) and intx + 1 (integer to the right of x)?
        let n0: f64 = 1.0 - 2.0*(self.perm[intx] as f64)/255.0;
        let n1: f64 = 1.0 - 2.0*(self.perm[(intx + 1) % 255] as f64)/255.0;

        // We compute the proportion used in the interpolation thanks to our shifted x
        let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0);

        // and we return the interpolated value
        return (1.0 - fx) * n0 + fx * n1;
    }
}

And that's it ! Visually, this code can give something like that.

A sample of 1D value noise.

Conclusion

This post was longer than I thought at the beginning, but I think it's really important to explain in details the value noise. Future noises will be based on that.

This implementation is not very optimal, but it's simple. In a second post, we'll make a slightly more optimal version of this 1D value noise, and see how to fractalize it. Then, we'll extend the idea of a value noise in 1D to more dimensions : 2D, 3D and 4D...