Improving the value noise.
Introduction
In this post, we'll improve the value noise we introduced last time in 3 steps :
- we'll improve the code for 1 dimension,
- we'll fractalize the noise,
- we'll extend the value noise in 2D, 3D, 4D.
With all the notions seen for the value noise, it will be considerably simpler to understand the next noises such as the Perlin Noise and the Simplex Noise.
Slight optimization
Here, I propose two slight optimizations/modifications for the value noise 1D, that will mainly prove to be useful when extending the noise to higher dimensions.
First note that we perform the exact same operations of addition and multiplications on n0 and n1 :
let n0: f64 = 1.0 - 2.0 * (self.perm[intx] as f64) / 255.0; let n1: f64 = 1.0 - 2.0 * (self.perm[(intx + 1) % 255] as f64) / 255.0;
and then we just add them multiplied by a scalar coefficient :
return (1.0 - fx) * n0 + fx * n1;
So we can avoid to do these operations twice (and four, eight or sixteen times in higher dimensions...) by just doing them once at the very end :
let n0: f64 = self.perm[intx] as f64; let n1: f64 = self.perm[(intx + 1) % 255] as f64; //... //<snip> //... return 1.0 - 2.0 *((1.0 - fx) * n0 + fx * n1)/255.0;
Another optimization is to get rid of this "modulo 255" for n1. It's here for only one case in 1D (if \(intx = 255\) exactly) but will be here more often in higher dimensions. To avoid it here and in higher dimensions, we double the size of the perm array by concatenating it with itself.
With those two optimizations we are almost ready to extend the value noise in 2D, 3D and 4D. We'll also create a general function noise that can take an array of 1 to 4 coordinates, and whose purpose is to call the right noise function.
A rust implementation could look like this :
pub fn noise(&self, position: &[f64]) -> f64 { if position.len() == 1 { let x = position[0]; self.noise1d(x) } else if position.len() == 2 { let x = position[0]; let y = position[1]; self.noise2d(x, y) } else if position.len() == 3 { let x = position[0]; let y = position[1]; let z = position[2]; self.noise3d(x, y, z) } else if position.len() == 4 { let x = position[0]; let y = position[1]; let w = position[2]; let z = position[3]; self.noise4d(x, y, z, w) } else { panic!( "Value Noise is implemented only for dimensions 1 to 4. Receive coordinates {:?}", position ) } }
With all these changes, our code looks like this for now :
Click to show the full rust implementation of value noise 1D.
// crate rand and rand_chacha // trait for shuffling use rand::seq::SliceRandom; // trait to construct a pseudo random number generator with a fixed seed. use rand::SeedableRng; // crate to create and save an image use image; pub struct ValueNoise { perm: [usize; 512], } impl ValueNoise { // Create and return a new value noise object pub fn new(seed: u64) -> Self { // seeding the pseudo-random number generator let mut rng = rand_chacha::ChaCha20Rng::seed_from_u64(seed); let mut perm = [0; 512]; let mut p = [0; 256]; //p = [0, 1, 2, ..., 254, 255] for i in 0..256 { p[i] = i as usize; } // we shuffle the array p.shuffle(&mut rng); // and we double it for i in 0..256 { perm[i] = p[i]; perm[i + 256] = p[i]; } // we return a new Value Noise object with a shuffled array, // ready to be used in the hash function return Self { perm: perm }; } // value noise at x pub fn noise1d(&self, x: f64) -> f64 { // left integer is intx let intx: f64 = x.floor(); // Next we shift the coordinates such that x is between 0 and 1 let x: f64 = x - intx; // We wrap the integer around a maximum of 255 let intx: usize = (intx as usize) % 255; // What are the values of the hash function for the index // intx (integer to the left of x) and // intx + 1 (integer to the right of x)? let n0: f64 = self.perm[intx] as f64; let n1: f64 = self.perm[intx + 1] as f64; // We compute the proportion used in the interpolation thanks to our shifted x let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); // and we return the interpolated value return 1.0 - 2.0 * ((1.0 - fx) * n0 + fx * n1) / 255.0; } fn noise2d(&self, x: f64, y: f64) -> f64 { // temporary self.noise1d(x) } fn noise3d(&self, x: f64, y: f64, z: f64) -> f64 { // temporary self.noise1d(x) } fn noise4d(&self, x: f64, y: f64, z: f64, w: f64) -> f64 { // temporary self.noise1d(x) } pub fn noise(&self, position: &[f64]) -> f64 { if position.len() == 1 { let x = position[0]; self.noise1d(x) } else if position.len() == 2 { let x = position[0]; let y = position[1]; self.noise2d(x, y) } else if position.len() == 3 { let x = position[0]; let y = position[1]; let z = position[2]; self.noise3d(x, y, z) } else if position.len() == 4 { let x = position[0]; let y = position[1]; let w = position[2]; let z = position[3]; self.noise4d(x, y, z, w) } else { panic!( "Value Noise is implemented only for dimensions 1 to 4. Receive coordinates {:?}", position ) } } } fn main() { // we'll draw the noise in an image of size (dimx, dimy) let dimx: u32 = 400; let dimy: u32 = 400; // the seed of our value noise let seed = 12; // the frequency of our output : expected value betwenn 0.0 and 256.0 // for bigger frequency, the value noise will repeat itself let freq = 4.0; // corresponding step for each pixel let dx = freq / dimx as f64; // Our seeded value noise object let noise = ValueNoise::new(seed); // we create a black image let mut imgbuf = image::ImageBuffer::new(dimx, dimy); for i in 0..dimx { // the value noise at x = i*dx let val = noise.noise1d(&[i as f64 * dx]); // we convert this value to an height in the image let j = ((val * (dimy as f64 - 1.0) / 2.0) + (dimy as f64 / 2.0)) as u32; // we set the corresponding pixel (i,j) to white let pixel = imgbuf.get_pixel_mut(i, j); *pixel = image::Luma([255 as u8]); } // we save the result imgbuf.save("value_noise_1D.png").unwrap(); }
Fractalization
For now we have only one level of details, it's our "raw" noise. To add some more, we add other layers of coherent noise on it. For that, we must introduce a vocabulary coming from waves in physics.
Amplitude
The amplitude \(A\) of a noise is the maximum value a noise can potentially reach (in absolute value). We fixed it to 1 for our value noise.
Wavelength
The wavelength \(w\) of a noise is the distance between each fixed values by the hash function. In our value noise the wavelength was \(w = 1\) because the hash function fixed the values of the noise at each integer, and integers are separated by a distance of 1.
We can create a new noise such that new_noise(\(x\)) = value_noise(\(2 \times x\)). The wavelength of that new noise would then be \(\frac{1}{2}\).
Frequency
The frequency \(f\) of a noise is the inverse of the wavelength.
\[f = \frac{1}{w}\]
The frequency of a new noise defined by new_noise(\(x\)) = value_noise(\(f \times x\)) is \(f\).
Octave
An octave is a layer of noise to be added with other layers to form the final fractalized noise.
This name comes from musical theory, a musical tone one octave higher than another has twice its frequency. By default, each octave of a fractalized noise has twice the frequency of the previous layer of noise.
Lacunarity
The lacunarity \(l\) of a fractalized noise is the number multiplying the frequency between each octave. That is, frequency(octave n+1) = \(l \times \) frequency(octave n)
By default \(l = 2\). So we are doubling the frequency between each octave of the fractalized noise.
Persistence
The persistence \(p\) of a fractalized noise is the number multiplying the amplitude between each octave. That is, amplitude(octave n+1) = \(p \times\) amplitude(octave n)
By default, \(p = \frac{1}{2}\). So we are halfing the amplitude between each octave of the fractalized noise.
Fractalization applied to the value noise
Our basic value noise looks like that :
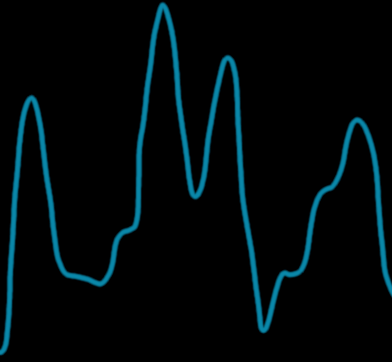
A sample of 1D value noise (octave 1).
To fractalize the value noise, we make that simple noise the base octave of our new noise. On top of it, we'll add other octaves of the same noise, with double the frequency and half the amplitude. Here we show the two next octaves of the same noise :
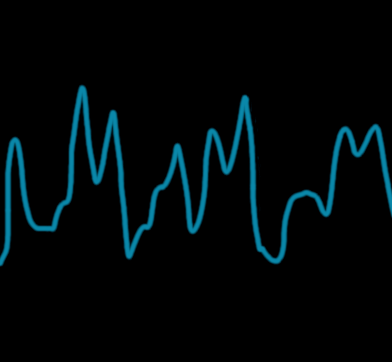
The second octave.
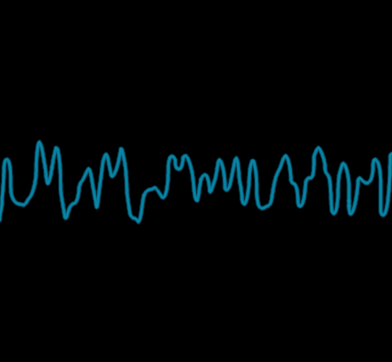
The third octave.
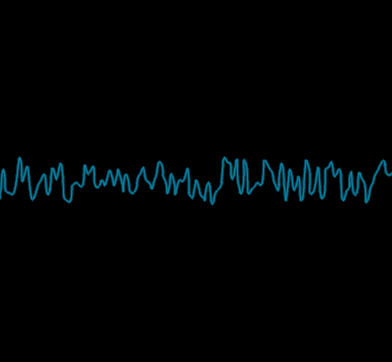
The fourth octave.
By adding the four octaves we obtain a fractalized noise with several level of details :
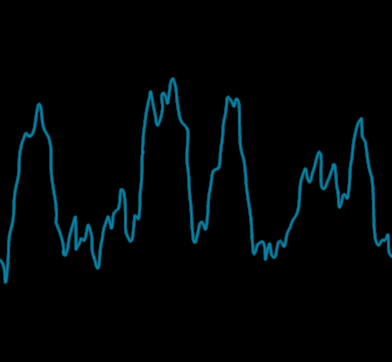
The fractalized noise.
As we want to keep our noises between -1 and 1, we divide the addition of octaves by \(\sum_{i=0}^{N-1} p^i \), with \(p\) the persistence and \(N\) the number of octaves of the fractalized noise.
For example, here, with \(p=\frac{1}{2} \), we added a noise of amplitude \(1\) (octave 1), \(\frac{1}{2} \) (octave 2), \(\frac{1}{4} \) (octave 3) and \(\frac{1}{8} \) (octave 4) ; so we divide the result by \(1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} = \frac{15}{8} \).
Notice the effect of fractalization on our noise :
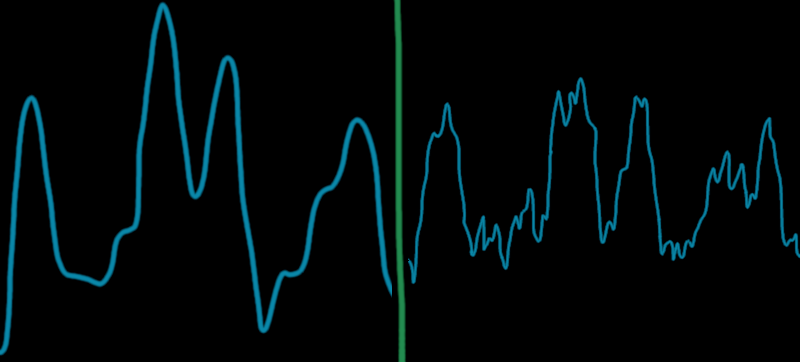
Comparison between the simple value noise and the fractalized value noise.
We still see the effect of the first octave as it's the more important, but we added considerably more details to it.
That's our fractalization method. By adding octaves we can choose to have a more complex noise result.
Fractalized noise in Rust
We modify our ValueNoise structure to add the number of octaves, lacunarity and persistence as attributes :
pub struct ValueNoise { perm: [usize; 512], num_octaves: u8, lacunarity: f64, persistence: f64, }
Of course we also modify the new function for this struct :
pub fn new(seed: u64, num_octaves: u8, lacunarity: f64, persistence: f64) -> Self { // snip // ... // we return a new Value Noise object with a shuffled array ready to be used in the hash function return Self { perm: perm, // expected to be at least 1 num_octaves: u8, // expected to be greater than 1.0 lacunarity: f64, // expected to be between 0.0 and 1.0 persistence: f64, }; }
Finally we rename the general noise function "noise_at_position", to replace the noise function with :
pub fn noise(&self, position: &[f64]) -> f64 { // simple value noise let mut res = self.noise_at_position(position); let mut max = 1.0; // if we have more than one octaves : if self.num_octaves > 1 { // We set the frequency and amplitude of the second octave let mut freq = self.lacunarity; let mut ampl = self.persistence; // We multiply the position by the frequence of the octave for _i in 0..(self.num_octaves - 1) { let mut new_pos: Vec<f64> = Vec::new(); for i in 0..position.len() { new_pos.push(position[i] * freq); } // We add the octave to the fractalized noise res += ampl * self.noise_at_position(&new_pos); max += ampl; // We set the frequency and amplitude of the next octave ampl *= self.persistence; freq *= self.lacunarity; } } res / max }
Our code looks like this now :
Click to show the full rust implementation of value noise 1D.
// trait for shuffling use rand::seq::SliceRandom; // trait to construct a pseudo random number generator with a fixed seed. use rand::SeedableRng; // crate to create and save an image use image; pub struct ValueNoise { perm: [usize; 512], // expected to be at least 1 num_octaves: u8, // expected to be greater than 1.0 lacunarity: f64, // expected to be between 0.0 and 1.0 persistence: f64, } impl ValueNoise { // Create and return a new value noise object pub fn new(seed: u64, num_octaves: u8, lacunarity: f64, persistence: f64) -> Self { // seeding the pseudo-random number generator let mut rng = rand_chacha::ChaCha20Rng::seed_from_u64(seed); let mut perm = [0; 512]; let mut p = [0; 256]; //p = [0, 1, 2, ..., 254, 255] for i in 0..256 { p[i] = i as usize; } // we shuffle the array p.shuffle(&mut rng); // and we double it for i in 0..256 { perm[i] = p[i]; perm[i + 256] = p[i]; } // we return a new Value Noise object with a shuffled array ready to be used in the hash function return Self { perm: perm, num_octaves: num_octaves, lacunarity: lacunarity, persistence: persistence, }; } // value noise at x fn noise1d(&self, x: f64) -> f64 { // left integer is intx let intx: f64 = x.floor(); // Next we shift the coordinates such that x is between 0 and 1 let x: f64 = x - intx; // We wrap the integer around a maximum of 255 let intx: usize = (intx as usize) % 255; // What are the values of the hash function for the index intx (integer to the left of x) and intx + 1 (integer to the right of x)? let n0: f64 = self.perm[intx] as f64; let n1: f64 = self.perm[intx + 1] as f64; // We compute the proportion used in the interpolation thanks to our shifted x let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); // and we return the interpolated value return 1.0 - 2.0 * ((1.0 - fx) * n0 + fx * n1) / 255.0; } fn noise2d(&self, x: f64, y: f64) -> f64 { // temporary self.noise1d(x) } fn noise3d(&self, x: f64, y: f64, z: f64) -> f64 { // temporary self.noise1d(x) } fn noise4d(&self, x: f64, y: f64, z: f64, w: f64) -> f64 { // temporary self.noise1d(x) } pub fn noise(&self, position: &[f64]) -> f64 { let mut res = self.noise_at_position(position); let mut max = 1.0; if self.num_octaves > 1 { let mut freq = self.lacunarity; let mut ampl = self.persistence; for _i in 0..(self.num_octaves - 1) { let mut new_pos: Vec<f64> = Vec::new(); for i in 0..position.len() { new_pos.push(position[i] * freq); } res += ampl * self.noise_at_position(&new_pos); max += ampl; ampl *= self.persistence; freq *= self.lacunarity; } } res / max } fn noise_at_position(&self, position: &[f64]) -> f64 { if position.len() == 1 { let x = position[0]; self.noise1d(x) } else if position.len() == 2 { let x = position[0]; let y = position[1]; self.noise2d(x, y) } else if position.len() == 3 { let x = position[0]; let y = position[1]; let z = position[2]; self.noise3d(x, y, z) } else if position.len() == 4 { let x = position[0]; let y = position[1]; let w = position[2]; let z = position[3]; self.noise4d(x, y, z, w) } else { panic!( "Value Noise is implemented only for dimensions 1 to 4. Receive coordinates {:?}", position ) } } } fn main() { // we'll draw the noise in an image of size (dimx, dimy) let dimx: u32 = 1000; let dimy: u32 = 1000; // the seed of our value noise let seed = 12; // the number of octaves of our value noise let num_octaves = 1; // the lacunarity of our value noise let lacunarity = 2.0; // the persistence of our value noise let persistence = 0.5; // the frequency of our output : expected value betwenn 0.0 and 256.0 // for bigger frequency, the value noise will repeat itself let freq = 12.0; // corresponding step for each pixel let dx = freq / dimx as f64; // Our seeded value noise object let noise = ValueNoise::new(seed, num_octaves, lacunarity, persistence); // we create a black image let mut imgbuf = image::ImageBuffer::new(dimx, dimy); for i in 0..dimx { // the value noise at x = i*dx let val = noise.noise(&[i as f64 * dx]); // we convert this value to an height in the image let j = ((val * (dimy as f64 - 1.0) / 2.0) + (dimy as f64 / 2.0)) as u32; // we set the corresponding pixel (i,j) to white let pixel = imgbuf.get_pixel_mut(i, j); *pixel = image::Luma([255 as u8]); } // we save the result imgbuf.save("value_noise_1D.png").unwrap(); }
We know how to fractalize any noise. Let's tacle the value noise in higher dimensions now.
Value Noise in higher dimensions
2D
To begin, let's copy the content of our 1D value noise into the 2D value noise function.
For a 2D value noise, we have two coordinates as an input : \(x\) and \(y\). Each pair \((x,y)\) is contained in a square delimited by 4 integers.
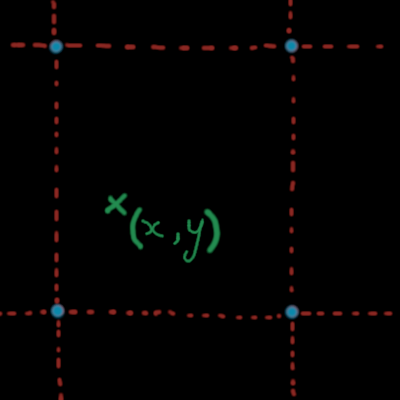
(x,y) in a grid.
The idea is very similar to 1D value noise : we fix the value of the noise for each pair of integers \((i,j)\), using a hash function ; and then for a pair of real numbers \((x,y)\), we interpolate the values of the four surrounding pairs of integers.
First, we perform the same computations for y that we did for x in 1D.
fn value2(&self, x: f64, y: f64) -> f64 { let intx: f64 = x.floor(); let inty: f64 = y.floor(); let x: f64 = x - intx; let y: f64 = y - inty; let intx: usize = (intx as usize) & 255; let inty: usize = (inty as usize) & 255; //snip }
Basically, we determine the indexes \((i,j)\) of the cell containing \((x,y)\).
Then, we use the same permutation table (that we extended in the optimization part) to get the 4 fixed values :
- n00 for the noise at \((i,j)\)
- n01 for the noise at \((i,j+1)\)
- n10 for the noise at \((i+1,j)\)
- n11 for the noise at \((i+1,j+1)\)
Our goal is to have a random value for these four points. One way to mix the coordinates in the permutation table is, for indexes \((i,j)\):
\[n00 = perm[i + perm[j]]\]
First we put the j index in the permutation table to obtain a value between 0 and 255, and we add it to the i index to obtain a value between 0 and 511 (hence our first optimization !) that goes itself into the permutation table to give a (pseudo-random) number between 0 and 255.
//snip let n00: f64 = self.perm[intx + self.perm[inty]] as f64; let n01: f64 = self.perm[intx + self.perm[inty + 1]] as f64; let n10: f64 = self.perm[intx + 1 + self.perm[inty]] as f64; let n11: f64 = self.perm[intx + 1 + self.perm[inty + 1]] as f64; //snip
Now we have to interpolate between four values. But our quintic Hermite spline only allows us to interpolate between two values ! No need to panic. We can decompose our interpolation dimension by dimension.
Let's get back to our cell, considering \((x,y)\) as local coordinates for the cell, therefore \((x,y) \in [0;1] \times [0;1] \).
There is some cases where the interpolation is as simple as the 1D case. For example, if \(y=0\):
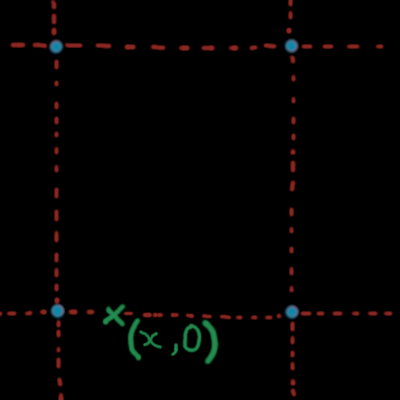
(x,0) in a grid.
In that case, the two upper integers don't affect the value of the noise. So we can compute the interpolation of that value as usual.
let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let nx0 = ifx * n00 + fx * n10;
The idea is the same with \(y=1\) : the two lower integers don't affect the value of the noise. So we can compute the interpolation of that value as usual.
let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let nx1 = ifx * n01 + fx * n11;
For \(y \in ]0;1[\), we just compute the interpolation along the y-axis between the two values nx0 and nx1, which are the interpolation along the x-axis when \(y\) is supposed to be 0 or 1 and doesn't play a role.
let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let fy = y * y * y * (y * (y * 6.0 - 15.0) + 10.0); let ifx = 1.0 - fx; // interpolated value on x-axis if y = 0 let nx0 = ifx * n00 + fx * n10; // interpolated value on x-axis if y = 1 let nx1 = ifx * n01 + fx * n11; // interpolated value on y-axis between nx0 and nx1 (1.0 - fy) * nx0 + fy * nx1 // it's between 0 and 255
Basically, in the next picture, we find nx0 and nx1 in the blue 1D interpolation, and after that we find the final interpolated value in the orange 1D interpolation.
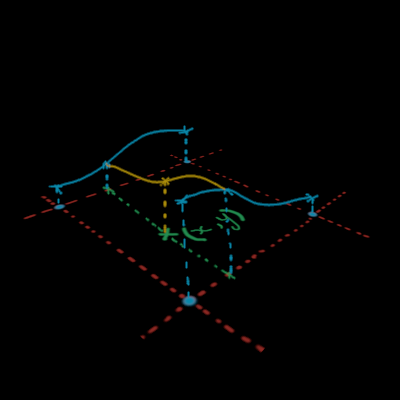
Interpolation in 2D.
And that's already done. The complete code for our 2D value noise is here :
fn value2(&self, x: f64, y: f64) -> f64 { // left integer is intx let intx: f64 = x.floor(); // bottom integer is inty let inty: f64 = y.floor(); // Next we shift the coordinates such that x and y are between 0 and 1 let x: f64 = x - intx; let y: f64 = y - inty; // We wrap the integers around a maximum of 255 let intx: usize = (intx as usize) & 255; let inty: usize = (inty as usize) & 255; // for the 4 integers-pairs around (x,y), we give a pseudo-random value from the hash function let n00: f64 = self.perm[intx + self.perm[inty]] as f64; let n01: f64 = self.perm[intx + self.perm[inty + 1]] as f64; let n10: f64 = self.perm[intx + 1 + self.perm[inty]] as f64; let n11: f64 = self.perm[intx + 1 + self.perm[inty + 1]] as f64; // We proceed to the interpolation let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let fy = y * y * y * (y * (y * 6.0 - 15.0) + 10.0); // first in the x-axis let ifx = 1.0 - fx; let nx0 = ifx * n00 + fx * n10; let nx1 = ifx * n01 + fx * n11; // then in the y-axis // We also scale the final value between -1.0 and 1.0 (2.0 * ((1.0 - fy) * nx0 + fy * nx1) / 255.0) - 1.0 }
The following picture has been realized with this code :
Click to show the full rust implementation of value noise 2D.
// trait for shuffling use rand::seq::SliceRandom; // trait to construct a pseudo random number generator with a fixed seed. use rand::SeedableRng; // crate to create and save an image use image; pub struct ValueNoise { perm: [usize; 512], // expected to be at least 1 num_octaves: u8, // expected to be greater than 1.0 lacunarity: f64, // expected to be between 0.0 and 1.0 persistence: f64, } impl ValueNoise { // Create and return a new value noise object pub fn new(seed: u64, num_octaves: u8, lacunarity: f64, persistence: f64) -> Self { // seeding the pseudo-random number generator let mut rng = rand_chacha::ChaCha20Rng::seed_from_u64(seed); let mut perm = [0; 512]; let mut p = [0; 256]; //p = [0, 1, 2, ..., 254, 255] for i in 0..256 { p[i] = i as usize; } // we shuffle the array p.shuffle(&mut rng); // and we double it for i in 0..256 { perm[i] = p[i]; perm[i + 256] = p[i]; } // we return a new Value Noise object with a shuffled array ready to be used in the hash function return Self { perm: perm, num_octaves: num_octaves, lacunarity: lacunarity, persistence: persistence, }; } // value noise at x fn noise1d(&self, x: f64) -> f64 { // left integer is intx let intx: f64 = x.floor(); // Next we shift the coordinates such that x is between 0 and 1 let x: f64 = x - intx; // We wrap the integer around a maximum of 255 let intx: usize = (intx as usize) % 255; // What are the values of the hash function for the index intx (integer to the left of x) and intx + 1 (integer to the right of x)? let n0: f64 = self.perm[intx] as f64; let n1: f64 = self.perm[intx + 1] as f64; // We compute the proportion used in the interpolation thanks to our shifted x let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); // and we return the interpolated value return 1.0 - 2.0 * ((1.0 - fx) * n0 + fx * n1) / 255.0; } fn noise2d(&self, x: f64, y: f64) -> f64 { // left integer is intx let intx: f64 = x.floor(); // bottom integer is inty let inty: f64 = y.floor(); // Next we shift the coordinates such that x and y are between 0 and 1 let x: f64 = x - intx; let y: f64 = y - inty; // We wrap the integers around a maximum of 255 let intx: usize = (intx as usize) & 255; let inty: usize = (inty as usize) & 255; // for the 4 integers-pairs around (x,y), we give a pseudo-random value from the hash function let n00: f64 = self.perm[intx + self.perm[inty]] as f64; let n01: f64 = self.perm[intx + self.perm[inty + 1]] as f64; let n10: f64 = self.perm[intx + 1 + self.perm[inty]] as f64; let n11: f64 = self.perm[intx + 1 + self.perm[inty + 1]] as f64; // We proceed to the interpolation let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let fy = y * y * y * (y * (y * 6.0 - 15.0) + 10.0); // first in the x-axis let ifx = 1.0 - fx; let nx0 = ifx * n00 + fx * n10; let nx1 = ifx * n01 + fx * n11; // then in the y-axis // We also scale the final value between -1.0 and 1.0 (2.0 * ((1.0 - fy) * nx0 + fy * nx1) / 255.0) - 1.0 } fn noise3d(&self, x: f64, y: f64, z: f64) -> f64 { // temporary self.noise1d(x) } fn noise4d(&self, x: f64, y: f64, z: f64, w: f64) -> f64 { // temporary self.noise1d(x) } pub fn noise(&self, position: &[f64]) -> f64 { let mut res = self.noise_at_position(position); let mut max = 1.0; if self.num_octaves > 1 { let mut freq = self.lacunarity; let mut ampl = self.persistence; for _i in 0..(self.num_octaves - 1) { let mut new_pos: Vec<f64> = Vec::new(); for i in 0..position.len() { new_pos.push(position[i] * freq); } res += ampl * self.noise_at_position(&new_pos); max += ampl; ampl *= self.persistence; freq *= self.lacunarity; } } res / max } fn noise_at_position(&self, position: &[f64]) -> f64 { if position.len() == 1 { let x = position[0]; self.noise1d(x) } else if position.len() == 2 { let x = position[0]; let y = position[1]; self.noise2d(x, y) } else if position.len() == 3 { let x = position[0]; let y = position[1]; let z = position[2]; self.noise3d(x, y, z) } else if position.len() == 4 { let x = position[0]; let y = position[1]; let w = position[2]; let z = position[3]; self.noise4d(x, y, z, w) } else { panic!( "Value Noise is implemented only for dimensions 1 to 4. Receive coordinates {:?}", position ) } } } fn main() { // we'll draw the noise in an image of size (dimx, dimy) let dimx: u32 = 400; let dimy: u32 = 400; // the seed of our value noise let seed = 12; // the number of octaves of our value noise let num_octaves = 1; // the lacunarity of our value noise let lacunarity = 2.0; // the persistence of our value noise let persistence = 0.5; // the frequency of our output : expected value betwenn 0.0 and 256.0 // for bigger frequency, the value noise will repeat itself let freq = 10.0; // corresponding step for each pixel let dx = freq / dimx as f64; // Our seeded value noise object let noise = ValueNoise::new(seed, num_octaves, lacunarity, persistence); // we create a black image let mut imgbuf = image::ImageBuffer::new(dimx, dimy); for i in 0..dimx { for j in 0..dimy { // the value noise at x = i*dx and y = j*dx let nxyzw = noise.noise(&[i as f64 * dx, j as f64 * dx]); // we scale the noise between 0 and 255 let gray = ((1.0 + nxyzw) * 127.5) as u8; // we set the corresponding pixel (i,j) to the scaled noise value let pixel = imgbuf.get_pixel_mut(i as u32, j as u32); *pixel = image::Luma([gray]); } } // we save the result imgbuf.save("value_noise_2D.png").unwrap(); }
A sample of 2D value noise.
And we can already add octaves to have a fractalized 2D value noise !

A sample of fractalized 2D value noise (4 octaves).
3D and 4D
There is no new ideas for 3D and 4D so I'll be very quick.
-
in 3D we use the \((x,y,z)\) coordinates and each point in \(\mathbb{R}^3\) is in a cell defined by 8 integers. The noise value at these integers is defined by the hash function.
-
in 4D we use the \((x,y,z,w)\) coordinates and each point in \(\mathbb{R}^4\) is in a cell defined by 16 integers. The noise value at these integers is defined by the hash function.
Click to show the rust implementation of value noise 3D and 4D.
fn noise3d(&self, x: f64, y: f64, z: f64) -> f64 { let intx: f64 = x.floor(); let inty: f64 = y.floor(); let intz: f64 = z.floor(); let x: f64 = x - intx; let y: f64 = y - inty; let z: f64 = z - intz; let intx: usize = (intx as usize) & 255; let inty: usize = (inty as usize) & 255; let intz: usize = (intz as usize) & 255; let n000: f64 = self.perm[intx + self.perm[inty + self.perm[intz]]] as f64; let n001: f64 = self.perm[intx + self.perm[inty + self.perm[intz + 1]]] as f64; let n010: f64 = self.perm[intx + self.perm[inty + 1 + self.perm[intz]]] as f64; let n011: f64 = self.perm[intx + self.perm[inty + 1 + self.perm[intz + 1]]] as f64; let n100: f64 = self.perm[intx + 1 + self.perm[inty + self.perm[intz]]] as f64; let n101: f64 = self.perm[intx + 1 + self.perm[inty + self.perm[intz + 1]]] as f64; let n110: f64 = self.perm[intx + 1 + self.perm[inty + 1 + self.perm[intz]]] as f64; let n111: f64 = self.perm[intx + 1 + self.perm[inty + 1 + self.perm[intz + 1]]] as f64; let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let fy = y * y * y * (y * (y * 6.0 - 15.0) + 10.0); let fz = z * z * z * (z * (z * 6.0 - 15.0) + 10.0); let ifx = 1.0 - fx; let ify = 1.0 - fy; let nx00 = ifx * n000 + fx * n100; let nx01 = ifx * n001 + fx * n101; let nx10 = ifx * n010 + fx * n110; let nx11 = ifx * n011 + fx * n111; let nxy0 = ify * nx00 + fy * nx10; let nxy1 = ify * nx01 + fy * nx11; (2.0 * ((1.0 - fz) * nxy0 + fz * nxy1) / 255.0) - 1.0 } fn noise4d(&self, x: f64, y: f64, z: f64, w: f64) -> f64 { let intx: f64 = x.floor(); let inty: f64 = y.floor(); let intz: f64 = z.floor(); let intw: f64 = w.floor(); let x: f64 = x - intx; let y: f64 = y - inty; let z: f64 = z - intz; let w: f64 = w - intw; let intx: usize = (intx as usize) & 255; let inty: usize = (inty as usize) & 255; let intz: usize = (intz as usize) & 255; let intw: usize = (intw as usize) & 255; let n0000: f64 = self.perm[intx + self.perm[inty + self.perm[intz + self.perm[intw]]]] as f64; let n0001: f64 = self.perm[intx + self.perm[inty + self.perm[intz + self.perm[intw + 1]]]] as f64; let n0010: f64 = self.perm[intx + self.perm[inty + self.perm[intz + 1 + self.perm[intw]]]] as f64; let n0011: f64 = self.perm[intx + self.perm[inty + self.perm[intz + 1 + self.perm[intw + 1]]]] as f64; let n0100: f64 = self.perm[intx + self.perm[inty + 1 + self.perm[intz + self.perm[intw]]]] as f64; let n0101: f64 = self.perm[intx + self.perm[inty + 1 + self.perm[intz + self.perm[intw + 1]]]] as f64; let n0110: f64 = self.perm[intx + self.perm[inty + 1 + self.perm[intz + 1 + self.perm[intw]]]] as f64; let n0111: f64 = self.perm [intx + self.perm[inty + 1 + self.perm[intz + 1 + self.perm[intw + 1]]]] as f64; let n1000: f64 = self.perm[intx + 1 + self.perm[inty + self.perm[intz + self.perm[intw]]]] as f64; let n1001: f64 = self.perm[intx + 1 + self.perm[inty + self.perm[intz + self.perm[intw + 1]]]] as f64; let n1010: f64 = self.perm[intx + 1 + self.perm[inty + self.perm[intz + 1 + self.perm[intw]]]] as f64; let n1011: f64 = self.perm [intx + 1 + self.perm[inty + self.perm[intz + 1 + self.perm[intw + 1]]]] as f64; let n1100: f64 = self.perm[intx + 1 + self.perm[inty + 1 + self.perm[intz + self.perm[intw]]]] as f64; let n1101: f64 = self.perm [intx + 1 + self.perm[inty + 1 + self.perm[intz + self.perm[intw + 1]]]] as f64; let n1110: f64 = self.perm [intx + 1 + self.perm[inty + 1 + self.perm[intz + 1 + self.perm[intw]]]] as f64; let n1111: f64 = self.perm [intx + 1 + self.perm[inty + 1 + self.perm[intz + 1 + self.perm[intw + 1]]]] as f64; let fx = x * x * x * (x * (x * 6.0 - 15.0) + 10.0); let fy = y * y * y * (y * (y * 6.0 - 15.0) + 10.0); let fz = z * z * z * (z * (z * 6.0 - 15.0) + 10.0); let fw = w * w * w * (w * (w * 6.0 - 15.0) + 10.0); let ifx = 1.0 - fx; let ify = 1.0 - fy; let ifz = 1.0 - fz; let nx000 = ifx * n0000 + fx * n1000; let nx001 = ifx * n0001 + fx * n1001; let nx010 = ifx * n0010 + fx * n1010; let nx011 = ifx * n0011 + fx * n1011; let nx100 = ifx * n0100 + fx * n1100; let nx101 = ifx * n0101 + fx * n1101; let nx110 = ifx * n0110 + fx * n1110; let nx111 = ifx * n0111 + fx * n1111; let nxy00 = ify * nx000 + fy * nx100; let nxy01 = ify * nx001 + fy * nx101; let nxy10 = ify * nx010 + fy * nx110; let nxy11 = ify * nx011 + fy * nx111; let nxyz0 = ifz * nxy00 + fz * nxy10; let nxyz1 = ifz * nxy01 + fz * nxy11; (2.0 * ((1.0 - fw) * nxyz0 + fw * nxyz1) / 255.0) - 1.0 }
Conclusion
We have a full implementation of the value noise. It allowed us to understand the concepts of permutation table, hash function, interpolation in any number of dimensions, and fractalization.
This noise is already great, but even in the fractalized version, we can "feel" the grid of integers. In 2D we still see the squares a little bit. An improvement of the value noise is the Perlin Noise, which is a kind of gradient noise. As we'll see in the next post, Perlin Noise allows us to blur or distord the grid we are using so it's not so obvious that we are using a grid. In 2D Perlin Noise, it's hard to see the squares for example. So, it's an improvement we'll develop in the next post.