Introduction

Just a small blog post to introduce the notion of noise, used particularly in texture synthesis for natural phenomenons. For this introduction, no need to have a mathematical background. In the next posts, I'll try to explain the maths behind noise functions, but that's for later.

Noise ?

The first time I heard about noise in a mathematical context was in a signal processing class. Basically, noise is everything unwanted. You want to record audio ? Noise will be everything that you didn't want to hear with your microphone ; it will be what your microphone gives when you think everything is silent. The name "noise" comes from acoustics and radio signals : you really want to send some information, but what is received is a little bit different. It's information, yes, but with noise. Your crystal-clear voice can become something almost inaudible. By extension, in signal processing, "noise" is the name given to everything that is not the information you wanted to send.

Often, noise is not in our beautiful, idealized mathematical models of informations. Noise comes from reality. From imperfect physical phenomenons that we will never be able to control exactly.

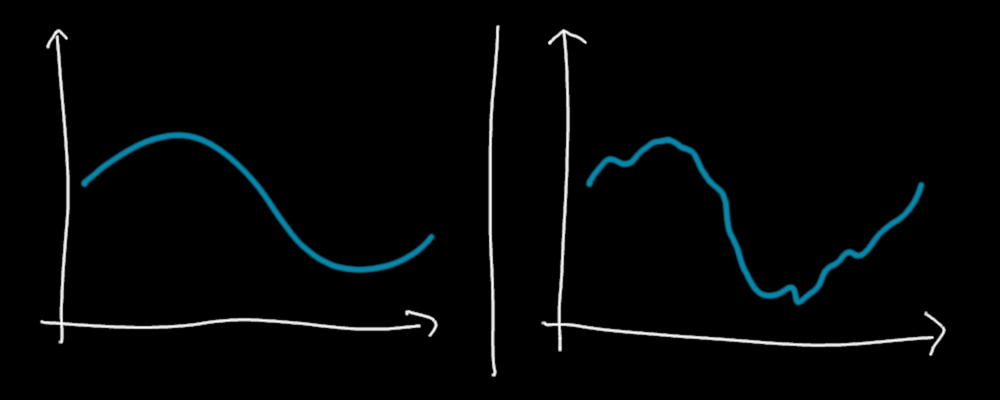
Left : theoretical signal you want to send. Right : the same information, but with noise. It's probably the signal that you send in reality.

Therefore, we study a lot noise and particularly noise reduction algorithm in signal processing. We want to get rid of that extra bit of unwanted information. It's just some random garbage, really.

One exception, though, and that's what will interest us here, is when you want to mimic reality. Reality is full of noise. Nothing is perfect. There is what we call "randomness" everywhere in nature. Let's take an example. You want to simulate a realistic, natural landscape. You will need noise. Have you ever seen a landscape like that in nature ?

A sinusoïdal landscape. Something that doesn't exist in nature.

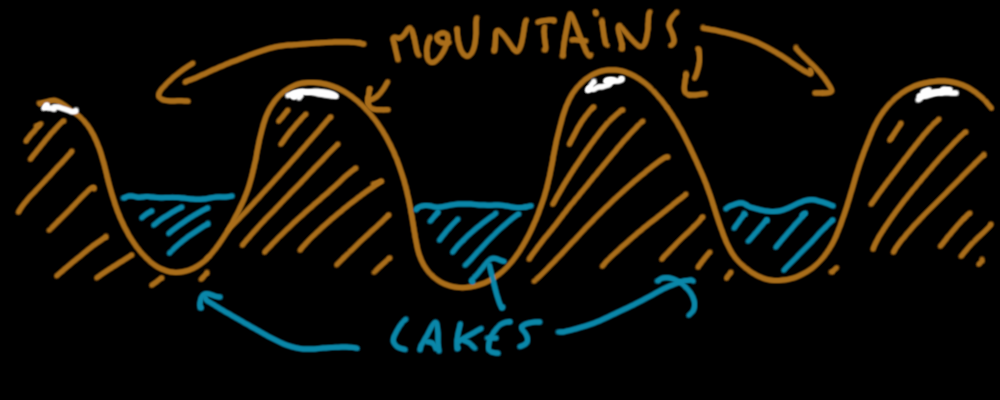
Of course not. You probably want more randomness to your landscape. Sometimes you'll want high mountains, hills, or sometimes lakes, maybe, but without a visible pattern of repeating ups and downs like the previous example. Take a look at this one :

A somewhat more natural landscape. Something that could exist in nature.

Isn't it better ? Isn't it a more believable landscape ? Notice however that the randomness in this landscape is quite special. It's not completely random. A completely random landscape would look like this :

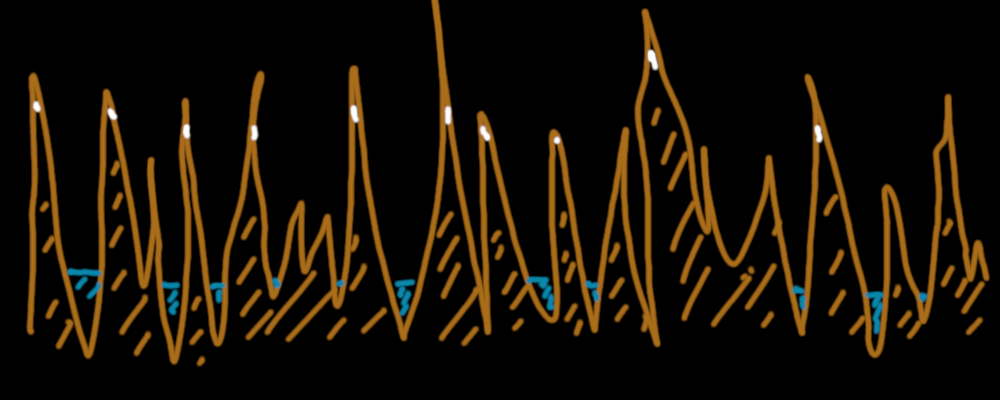
A completely random landscape. It's not natural at all, but in a different way than the mathematical idealization of a landscape.

We see that we need a coherent noise. If we have the peak of a mountain at one point, there's no chance to find a deep sea nearby. We have first to walk down the mountain. It takes some times. Here, coherent means "continuous", "smooth". The height at one point is correlated to the height of neighbour points.

One last point. Many things in nature are fractal. If you don't know what does that mean, don't worry. Just think of "something with various levels of details". To continue with landscape, at a low level of details, we can consider only mountains and big variations in height.

Fractal construction of a landscape. First, big variations.

Then we can consider hills, which are medium variations of the landscape.

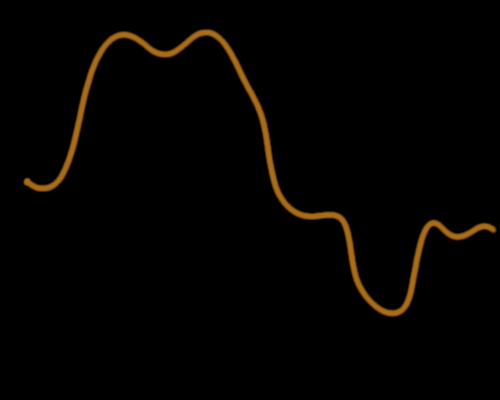
Fractal construction of a landscape. Second, medium variations.

But we'll also have boulders that locally will change the height.

Fractal construction of a landscape. Third, small variations.

But if we zoom in, the stones will also give small variations :

Fractal construction of a landscape. Finally, very small variations.

And we could go on and on...

Our goal with noise

In this series of articles, we'll design noise algorithms in the Rust programming language. Our algorithms will share some specificities :

• they will be random at a large scale, however they will produce a coherent noise, a very special kind of randomness that is smooth and continous,
• they will be reproducible : with the same input, we'll always give the same noise,
• they will have the possibility to give an output with various levels of details (fractal noise),
• they will be able to produce noise in 1, 2, 3 and 4 dimensions.
• they will give a random value between -1 and 1.

These noise algorithms have several applications in procedural content generation. We can make landscapes, clouds, fire, water surfaces, smooth animations... The possibilities are infinite, really. For example, a 4D noise can simulate a 3D cloud smoothly animated, considering the time to be the fourth dimension.

In the next post, we'll make a value noise. They are probably the simplest kind of noise and a very good opportunity to present the basic concepts of noise generation that will be shared by all our noise algorithms.

---